Long-Range 2020 Election Forecast - March Update

A little over five months ago, I posted a forecast of what would happen in the 2020 presidential election based on a long-range election forecast model that I developed back in 2015.  That forecast suggested a strong possibility of Democratic victory in 2020, but it really depended upon who won the nomination.

That forecast indicated that Biden, Sanders, and Warren all stood the best chance of defeating Trump in November, but that Biden was best positioned.  It was much less bullish on Harris and Buttigieg.  Klobuchar and Bloomberg weren't even on the radar yet.

A lot has happened since November 2019, as often happens during the nomination phase of a Presidential Election cycle. The Democratic field has winnowed down to essentially two candidates, Joe Biden and Bernie Sanders. (Sorry, Tulsi) So, there's really two questions to ask at this point:

1. Has anything changed since November?
2. Does it matter which candidate the Democrats nominate?

The answer to the first question is simple: Not much.  The only thing that has really changed is that it's a lot easier for me to generate the forecasts because now there's only two candidates for which I need to generate forecasts.  Beyond that, the forecast hasn't shifted much since November.  So the answer to the second question also seems to be "Not much."

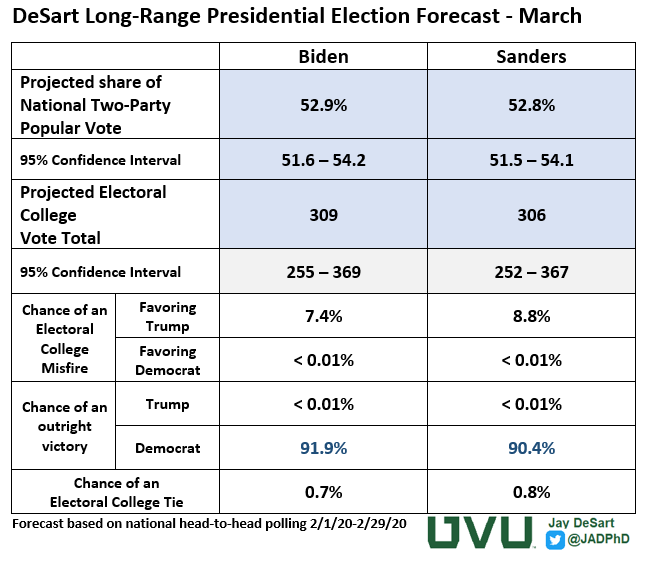
Both Biden and Sanders are projected to win the popular vote with ease under this update. The only real shift is that the model is slightly more bullish on their chances at winning the Electoral College as well.

While the projected Electoral College vote totals are slightly higher for both Biden and Sanders than they were 5 months ago, the 95% confidence intervals still leave open the possibility for Trump to win reelection.  Simply put, there's more than an insignificant chance that Donald Trump could win a second term. The interesting thing about that is that the model suggests that pretty much the only path to victory for Trump is through a repeat of 2016: an Electoral College misfire where the Democrat wins the popular vote but Trump wins at least 270 Electoral Votes and claims victory.

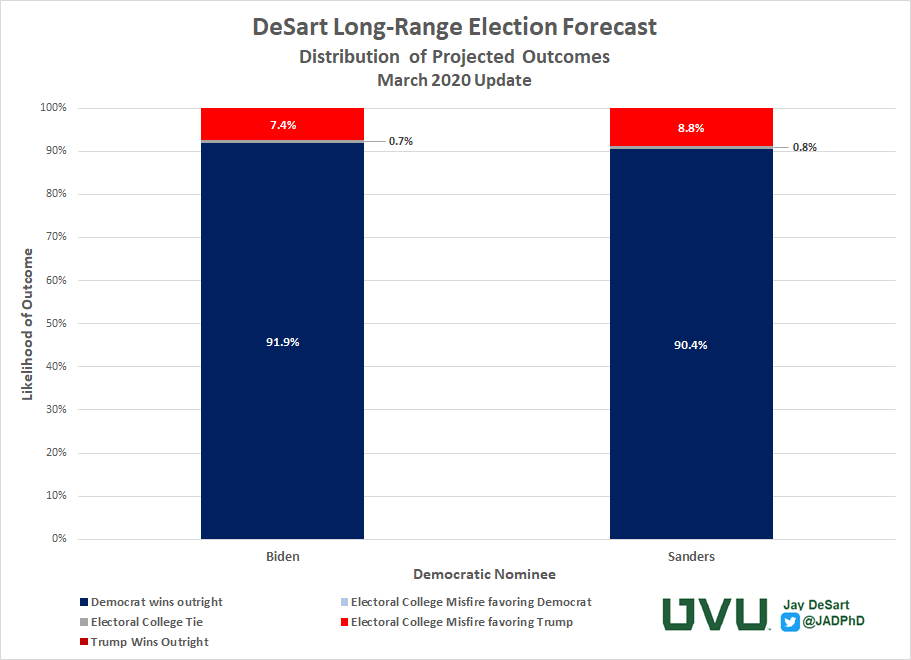
Using the model's point estimates for each of the state-level outcomes, and factoring in its level of prediction error, I ran a simulation of 100,000 elections for each potential pairing to get a range of possible outcomes.  The breakdown of those 100,000 simulated elections is shown in the bottom half of the table above.  In addition, the chart below presents how often each possible outcome appeared.

Out of the 100,000 simulated elections between Joe Biden and Donald Trump, Biden won both the popular vote and Electoral College vote 91.9% of the time.  In none of those elections did the same happen for Trump.  Every single one of the simulated elections where Trump defeated Biden in the Electoral College, it came when he lost the popular vote. 

The outcomes were similar in the matchup between Bernie Sanders and Donald Trump, although there was a slightly lower occurrence of an outright Sanders victory (90.4%), and a slightly higher occurrence of an Electoral College misfire benefiting Trump. (8.4%).  Regardless of which candidate the Democrats nominate, this model suggests that there is a very slight, (less than 1%) of an Electoral College 269-269 tie, necessitating a vote by the U.S. House of Representatives to determine the winner.

For comparison purposes, when I used this model in March of 2016 and generated a similar distribution of possible outcomes, the model projected an Electoral College victory for Donald Trump 66.3% of the time.  Simply put, the model saw a Trump victory in 2016 as much more likely than a repeat performance in 2020.

We'll just have to wait another eight months to see how well this projection holds up. A lot can happen between now and then, and that could alter the context and trajectory of this race. I will be posting periodic updates to the forecast in that time.

So, stay tuned. In the meantime, I'll keep looking at the numbers, because that's what a nerd does.